NACA airfoil wing model - nonintrusive computation

Finite element Model
Generate model
Dynamical system setup
Linear Modal analysis and SSM setup
Forced response curves using SSMs

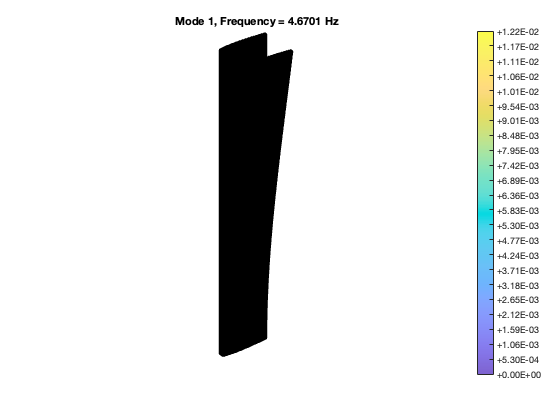
Finite element Model

Finite element model from the following reference:

Jain, S., Tiso, P., Rutzmoser, J. B., & Rixen, D. J. (2017). A quadratic manifold for model order reduction of nonlinear structural dynamics. Computers & Structures, 188, 80�94. <https://doi.org/10.1016/J.COMPSTRUC.2017.04.005>

Finite element code taken from the following package:

Jain, S., Marconi, J., Tiso P. (2020). YetAnotherFEcode (Version v1.1). Zenodo. <http://doi.org/10.5281/zenodo.4011282>

clear all; close all; clc
run ../../install.m
% change to example directory
exampleDir = fileparts(mfilename('fullpath'));
cd(exampleDir)

system parameters

epsilon = 1;

Generate model

[M,C,K,fnl,f_0,outdof] = build_model_nonIntrusive();
n = length(M);
disp(['Number of degrees of freedom = ' num2str(n)])
disp(['Phase space dimensionality = ' num2str(2*n)])

Reading mesh from Wing.msh
Building FE model
Assembling M,C,K matrices
Applying boundary conditions
Solving undamped eigenvalue problem

ans = 

  Patch (Deformed Mesh) with properties:

    FaceColor: 'interp'
    FaceAlpha: 1
    EdgeColor: [0 0 0]
    LineStyle: '-'
        Faces: [49968×3 double]
     Vertices: [149904×3 double]

  Use GET to show all properties

Using Rayleigh damping
Assembling external force vector
Getting nonlinearity function
Number of degrees of freedom = 133920
Phase space dimensionality = 267840

Dynamical system setup

We consider the forced system

$\mathbf{M}\ddot{\mathbf{x}}+\mathbf{C}\dot{\mathbf{x}}+\mathbf{K}\mathbf{x}+\mathbf{f}(\mathbf{x},\dot{\mathbf{x}})=\epsilon\mathbf{f}^{ext}(\mathbf{\Omega}t),$

which can be written in the first-order form as

$\mathbf{B}\dot{\mathbf{z}}=\mathbf{Az}+\mathbf{F}(\mathbf{z})+\epsilon\mathbf{F}^{ext}(\mathbf{\phi}),\\\dot{\mathbf{\phi}} =\mathbf{\Omega}$

where

$\mathbf{z}=\left[\begin{array}{c}\mathbf{x}\\\dot{\mathbf{x}}\end{array}\right],\quad\mathbf{A}=\left[\begin{array}{cc}-\mathbf{K} & \mathbf{0}\\\mathbf{0} & \mathbf{M}\end{array}\right],\mathbf{B}=\left[\begin{array}{cc}\mathbf{C} & \mathbf{M}\\\mathbf{M} & \mathbf{0}\end{array}\right],\quad\quad\mathbf{F}(\mathbf{z})=\left[\begin{array}{c}\mathbf{-\mathbf{f}(\mathbf{x},\dot{\mathbf{x}})}\\\mathbf{0}\end{array}\right],\quad\mathbf{F}^{ext}(\mathbf{z},\mathbf{\phi})=\left[\begin{array}{c}\mathbf{f}^{ext}(\mathbf{\phi})\\\mathbf{0}\end{array}\right]$ .

DSorder = 2;
DS = DynamicalSystem(DSorder);
set(DS,'M',M,'C',C,'K',K,'fnl_non',fnl);
set(DS.Options,'Emax',5,'Nmax',10,'notation','multiindex')
set(DS.Options,'Intrusion','none')

% set(DS.Options,'Emax',5,'Nmax',10,'notation','tensor')

We assume periodic forcing of the form

$\mathbf{f}^{ext}(\phi) = \mathbf{f}_0\cos(\phi)=\frac{\mathbf{f}_0}{2}e^{i\phi} + \frac{\mathbf{f}_0}{2}e^{-i\phi}$

Fourier coefficients of Forcing

kappas = [-1; 1];
coeffs = [f_0 f_0]/2;
DS.add_forcing(coeffs, kappas,epsilon);

Linear Modal analysis and SSM setup

[V,D,W] = DS.linear_spectral_analysis();

Due to high-dimensionality, we compute only the first 5 eigenvalues with the smallest magnitude. These would also be used to compute the spectral quotients
Assuming a proportional damping hypthesis with symmetric matrices
modal damping ratio for 1 mode is 2.000000e-03
modal damping ratio for 2 mode is 2.000000e-03
modal damping ratio for 3 mode is 2.264041e-03
modal damping ratio for 4 mode is 3.612822e-03
modal damping ratio for 5 mode is 5.538531e-03
the left eigenvectors may be incorrect in case of asymmetry of matrices

 The first 10 nonzero eigenvalues are given as 
   1.0e+02 *

  -0.0006 + 0.2934i
  -0.0006 - 0.2934i
  -0.0030 + 1.5226i
  -0.0030 - 1.5226i
  -0.0041 + 1.8088i
  -0.0041 - 1.8088i
  -0.0113 + 3.1381i
  -0.0113 - 3.1381i
  -0.0274 + 4.9385i
  -0.0274 - 4.9385i

Choose Master subspace (perform resonance analysis)

S = SSM(DS);
set(S.Options, 'reltol', 0.1,'notation','multiindex')
% set(S.Options, 'reltol', 0.1,'notation','tensor')
masterModes = [1,2];
S.choose_E(masterModes);

No (near) outer resonances detected in the (truncated) spectrum
sigma_out = 46
(near) inner resonance detected for the following combination of master eigenvalues
     2     1
     3     2
     4     3
     5     4
     1     2
     2     3
     3     4
     4     5

These are in resonance with the follwing eigenvalues of the master subspace
  -0.0587 +29.3428i
  -0.0587 +29.3428i
  -0.0587 +29.3428i
  -0.0587 +29.3428i
  -0.0587 -29.3428i
  -0.0587 -29.3428i
  -0.0587 -29.3428i
  -0.0587 -29.3428i

sigma_in = 46

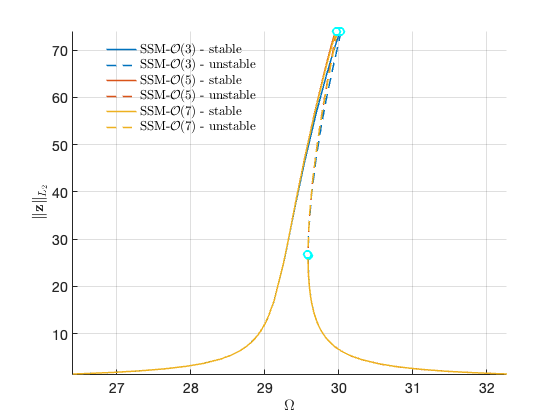
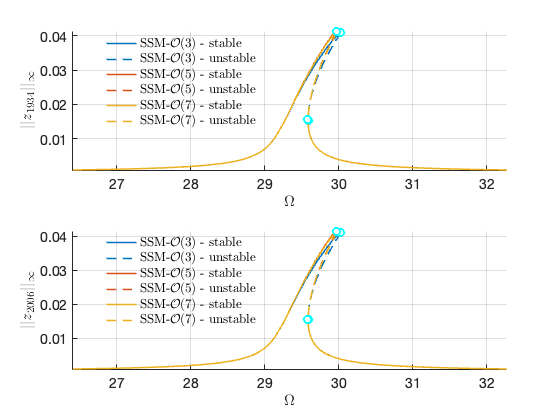
Forced response curves using SSMs

Obtaining forced response curve in reduced-polar coordinate

order = [3 5 7]; % Approximation order

setup options

set(S.Options, 'reltol', 1,'IRtol',0.02,'notation', 'multiindex','contribNonAuto',false)
set(S.FRCOptions, 'nt', 2^7, 'nRho', 200, 'nPar', 200, 'nPsi', 100, 'rhoScale', 2 )
% set(S.FRCOptions, 'method','level set')
set(S.FRCOptions, 'method','continuation ep', 'z0', 1e-4*[1; 1])
set(S.FRCOptions, 'outdof',outdof)

choose frequency range around the first natural frequency

omega0 = imag(S.E.spectrum(1));
omegaRange = omega0*[0.9 1.1];

extract forced response curve

FRC = S.extract_FRC('freq',omegaRange,order);
figFRC = gcf;

*****************************************
Calculating FRC using SSM with master subspace: [1  2]
(near) outer resonance detected for the following combination of master eigenvalues
     5     0
     6     0
     6     1
     7     1
     7     2
     8     2
     0     5
     0     6
     1     6
     1     7
     2     7
     2     8
     6     0
     7     0
     7     1
     8     1
     8     2
     0     6
     0     7
     1     7
     1     8
     2     8
    10     0
     0    10

These are in resonance with the follwing eigenvalues of the slave subspace
   1.0e+02 *

  -0.0030 + 1.5226i
  -0.0030 + 1.5226i
  -0.0030 + 1.5226i
  -0.0030 + 1.5226i
  -0.0030 + 1.5226i
  -0.0030 + 1.5226i
  -0.0030 - 1.5226i
  -0.0030 - 1.5226i
  -0.0030 - 1.5226i
  -0.0030 - 1.5226i
  -0.0030 - 1.5226i
  -0.0030 - 1.5226i
  -0.0041 + 1.8088i
  -0.0041 + 1.8088i
  -0.0041 + 1.8088i
  -0.0041 + 1.8088i
  -0.0041 + 1.8088i
  -0.0041 - 1.8088i
  -0.0041 - 1.8088i
  -0.0041 - 1.8088i
  -0.0041 - 1.8088i
  -0.0041 - 1.8088i
  -0.0113 + 3.1381i
  -0.0113 - 3.1381i

sigma_out = 46
(near) inner resonance detected for the following combination of master eigenvalues
     2     1
     3     2
     4     3
     5     4
     1     2
     2     3
     3     4
     4     5

These are in resonance with the follwing eigenvalues of the master subspace
  -0.0587 +29.3428i
  -0.0587 +29.3428i
  -0.0587 +29.3428i
  -0.0587 +29.3428i
  -0.0587 -29.3428i
  -0.0587 -29.3428i
  -0.0587 -29.3428i
  -0.0587 -29.3428i

sigma_in = 46
Due to (near) outer resonance, the exisitence of the manifold is questionable and the underlying computation may suffer.
Attempting manifold computation
Manifold computation time at order 2 = 00:02:19
Estimated memory usage at order  2 = 2.29E+02 MB
Manifold computation time at order 3 = 00:04:04
Estimated memory usage at order  3 = 2.46E+02 MB
Manifold computation time at order 4 = 00:10:19
Estimated memory usage at order  4 = 2.78E+02 MB
Manifold computation time at order 5 = 00:16:38
Estimated memory usage at order  5 = 2.91E+02 MB
Manifold computation time at order 6 = 00:38:37
Estimated memory usage at order  6 = 3.19E+02 MB
Manifold computation time at order 7 = 00:55:32
Estimated memory usage at order  7 = 3.35E+02 MB

 Run='freqSubint1Order3.ep': Continue equilibria along primary branch.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          2.20e-02  4.17e+01    0.0    0.0    0.0
   1   1  1.00e+00  9.79e-02  1.10e-04  4.17e+01    0.0    0.0    0.0
   2   1  1.00e+00  1.10e-03  4.97e-08  4.17e+01    0.0    0.0    0.0
   3   1  1.00e+00  1.74e-07  9.88e-16  4.17e+01    0.0    0.1    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1          th1          eps
    0  00:00:00   4.1699e+01      1  EP      2.9343e+01   7.5879e-01   2.7048e+00   1.0000e+00
   10  00:00:01   4.0892e+01      2          2.8745e+01   1.7381e-01   3.0448e+00   1.0000e+00
   20  00:00:01   3.7621e+01      3  EP      2.6409e+01   3.5977e-02   3.1216e+00   1.0000e+00

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1          th1          eps
    0  00:00:01   4.1699e+01      4  EP      2.9343e+01   7.5879e-01   2.7048e+00   1.0000e+00
   10  00:00:01   4.2598e+01      5          3.0015e+01   1.7601e+00   1.6752e+00   1.0000e+00
   14  00:00:01   4.2609e+01      6  SN      3.0030e+01   1.7677e+00   1.5257e+00   1.0000e+00
   14  00:00:01   4.2609e+01      7  FP      3.0030e+01   1.7677e+00   1.5257e+00   1.0000e+00
   20  00:00:01   4.2526e+01      8          2.9988e+01   1.6911e+00   1.2675e+00   1.0000e+00
   30  00:00:01   4.1867e+01      9  FP      2.9587e+01   6.3662e-01   3.6246e-01   1.0000e+00
   30  00:00:01   4.1867e+01     10  SN      2.9587e+01   6.3657e-01   3.6243e-01   1.0000e+00
   30  00:00:01   4.1867e+01     11          2.9587e+01   6.3444e-01   3.6115e-01   1.0000e+00
   40  00:00:01   4.2110e+01     12          2.9766e+01   2.5560e-01   1.4258e-01   1.0000e+00
   50  00:00:01   4.3587e+01     13          3.0812e+01   7.1868e-02   3.9952e-02   1.0000e+00
   55  00:00:02   4.5658e+01     14  EP      3.2277e+01   3.5984e-02   1.9999e-02   1.0000e+00
Time spent on mapping the FRC to physical coordinates maptime 54.8088 seconds. 

 Run='freqSubint1Order5.ep': Continue equilibria along primary branch.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          1.69e-04  4.17e+01    0.0    0.0    0.0
   1   1  1.00e+00  6.15e-04  3.90e-09  4.17e+01    0.0    0.0    0.0
   2   1  1.00e+00  3.57e-08  5.55e-17  4.17e+01    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1          th1          eps
    0  00:00:00   4.1699e+01      1  EP      2.9343e+01   7.6294e-01   2.7023e+00   1.0000e+00
   10  00:00:00   4.0899e+01      2          2.8750e+01   1.7527e-01   3.0440e+00   1.0000e+00
   20  00:00:00   3.7621e+01      3  EP      2.6409e+01   3.5977e-02   3.1216e+00   1.0000e+00

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1          th1          eps
    0  00:00:00   4.1699e+01      4  EP      2.9343e+01   7.6294e-01   2.7023e+00   1.0000e+00
   10  00:00:00   4.2509e+01      5          2.9952e+01   1.7599e+00   1.6738e+00   1.0000e+00
   14  00:00:00   4.2517e+01      6  SN      2.9966e+01   1.7663e+00   1.5151e+00   1.0000e+00
   14  00:00:00   4.2517e+01      7  FP      2.9966e+01   1.7663e+00   1.5151e+00   1.0000e+00
   20  00:00:00   4.2436e+01      8          2.9926e+01   1.6745e+00   1.2373e+00   1.0000e+00
   30  00:00:00   4.1865e+01      9  SN      2.9586e+01   6.4218e-01   3.6579e-01   1.0000e+00
   30  00:00:00   4.1865e+01     10  FP      2.9586e+01   6.4202e-01   3.6569e-01   1.0000e+00
   30  00:00:00   4.1870e+01     11          2.9591e+01   5.4940e-01   3.1081e-01   1.0000e+00
   40  00:00:00   4.2151e+01     12          2.9796e+01   2.3753e-01   1.3244e-01   1.0000e+00
   50  00:00:00   4.4036e+01     13          3.1130e+01   5.9067e-02   3.2833e-02   1.0000e+00
   54  00:00:00   4.5658e+01     14  EP      3.2277e+01   3.5984e-02   1.9999e-02   1.0000e+00
Time spent on mapping the FRC to physical coordinates maptime 84.3043 seconds. 

 Run='freqSubint1Order7.ep': Continue equilibria along primary branch.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          1.64e-04  4.17e+01    0.0    0.0    0.0
   1   1  1.00e+00  5.92e-04  3.57e-09  4.17e+01    0.0    0.0    0.0
   2   1  1.00e+00  3.26e-08  2.78e-17  4.17e+01    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1          th1          eps
    0  00:00:00   4.1699e+01      1  EP      2.9343e+01   7.6281e-01   2.7023e+00   1.0000e+00
   10  00:00:00   4.0899e+01      2          2.8750e+01   1.7522e-01   3.0440e+00   1.0000e+00
   20  00:00:00   3.7621e+01      3  EP      2.6409e+01   3.5977e-02   3.1216e+00   1.0000e+00

 STEP      TIME        ||U||  LABEL  TYPE            om         rho1          th1          eps
    0  00:00:00   4.1699e+01      4  EP      2.9343e+01   7.6281e-01   2.7023e+00   1.0000e+00
   10  00:00:00   4.2525e+01      5          2.9963e+01   1.7605e+00   1.6731e+00   1.0000e+00
   14  00:00:00   4.2533e+01      6  SN      2.9977e+01   1.7671e+00   1.5183e+00   1.0000e+00
   14  00:00:00   4.2533e+01      7  FP      2.9977e+01   1.7671e+00   1.5183e+00   1.0000e+00
   20  00:00:00   4.2450e+01      8          2.9936e+01   1.6785e+00   1.2439e+00   1.0000e+00
   30  00:00:00   4.1865e+01      9  SN      2.9586e+01   6.4199e-01   3.6568e-01   1.0000e+00
   30  00:00:00   4.1865e+01     10  FP      2.9586e+01   6.4179e-01   3.6555e-01   1.0000e+00
   30  00:00:00   4.1868e+01     11          2.9590e+01   5.6246e-01   3.1848e-01   1.0000e+00
   40  00:00:00   4.2144e+01     12          2.9791e+01   2.4036e-01   1.3402e-01   1.0000e+00
   50  00:00:00   4.3924e+01     13          3.1051e+01   6.1807e-02   3.4357e-02   1.0000e+00
   54  00:00:00   4.5658e+01     14  EP      3.2277e+01   3.5984e-02   1.9999e-02   1.0000e+00
Time spent on mapping the FRC to physical coordinates maptime 113.5491 seconds. 
Total time spent on FRC computation upto O(3) = 00:10:51
Total time spent on FRC computation upto O(5) = 00:37:52
Total time spent on FRC computation upto O(7) = 02:12:02